Screw the power law, embrace the power law

A couple of notable developments in the whole power laws and weblog discussion. Steven Johnson states that, ok, the distribution of influence in the weblog world follows a power law…now what? If we as participants in that network don’t want things to work that way, is there anything we can do about it?

Prompted by all the power law talk, David Sifry is now using non-linear equations to determine recent interesting weblogs and recent interesting newcomers for Technorati. The idea is that the distribution of weblogs is non-linear (the power law curve isn’t a straight line), so why not use non-linear equations to level the playing field a little.

What David is doing is actually why I graphed the Technorati data in the first place. I was trying to figure out how you could make the interesting blogs list not favor the top-linked sites all the time (200 new sites linking to Movable Type is not interesting considering it already has 6000 sites linking to it).

Here’s an email I sent David a couple of days ago:

“I started thinking about [the graph of the data] in relation to the Interesting Recent Blogs list and how it could be made more useful. Because it’s the biggest, Google is always going to be at the top of the list, and some little weblog with 4 new posts (out of a total of 6) is never going to get anywhere near the top. I was thinking that by analyzing the distribution of the links, you could introduce a adjustment factor based on the rank of the site relative to the #1 site. The problem is, I can’t remember enough of my college math to get from the power law equation to this magical adjustment factor. You might have better luck.”

The idea is that instead of using a quadratic or cubic equation that kinda fits the data, you use a power law equation generated by the data itself to exactly fit the data (or nearly so). The power law equation I derived using the limited sample of the top 100 list is:

y = 5989.8x^(-0.8309)

where y is the # of inbound blogs and x is the rank of the site. I plotted the top 100 data again and tried to fit three curves to it:

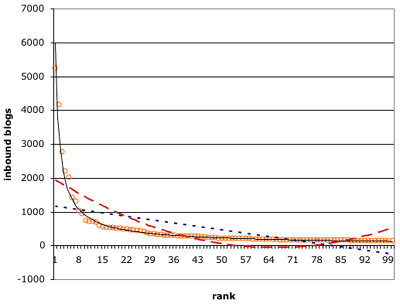
The dotted blue line is a linear equation, the dashed red line is a quadratic equation, and the solid black line is the aforementioned power law equation. As you can see, the linear and quadratic equations fit the data poorly. The R-squared for the linear equation is 0.31, 0.55 for the quadratic, and 0.99 for the power law equation. So the quadratic is an improvement over the linear equation, but neither compare to the excellent fit of the power law and the excellent results that would follow from using it for Technorati’s interesting recent blogs lists.